题目

现有一个含有n个正整数的数列，从中选择任意个数，但选了第i个数，就不能选第i-1和第i+1的数,求选择的数的最大和。
输入第一行为一个n，表示数的个数，第二行为n个数表示数列
输出选数最大和。
样例输入：
5
4 1 1 9 1
样例输出:
13

思路

先根据题意想递推式，从左到右遍历，每一个数都有选与不选两个选项，那么求前i个数的最大选数和opt(i)，可以分为选第i个数和不选,如果选了，那么最大和就为nums[i]+opt(i-2),如果不选就为opt(i-1),取这两个值中较大的数，就是前i个数的最大选数和了，再来想下递归出口，当i=1时，那么最大选数和肯定就是选第一个数了，所以opt(1) = nums1,而当i=2时，最大选数和就为nums1和nums[2]中较大值了。根据这些就可以写出最大选数和公式:

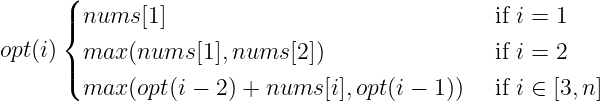
套用这个公式，opt(n)就是最大选数和了，但是在递归过程中，会计算大量重复的opt(i),容易超时，所以就需要用动规优化一下，把计算过的opt(i)的值存进f[i]中，如果f[i]有值，那么opt(i)直接返回f[i]即可。
递归代码如下：

#include<iostream>
#include<algorithm>

using namespace std;

int n;
int nums[1005];
int f[1006];        //1~i的最大可选和 
//返回1~i中最大选数和 
int opt(int i){
    if(i == 1)return nums[i];
    if(i == 2)return max(nums[1],nums[2]);
    if(f[i]!=0)return f[i];
    int choose = 0,noChoose = 0;
    choose = nums[i] + opt(i-2);
    noChoose = opt(i-1);
    f[i] = max(choose,noChoose);
    return f[i]; 
}
int main(){
    //加快读写 
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    cin >> n;
    for(int i = 1;i <= n;++i)
        cin >> nums[i];
    cout << opt(n) << endl;

    return 0;
}

非递归代码如下：

#include<iostream>
#include<algorithm>

using namespace std;


int n;
int nums[1005];
int f[1006];        //1~i的最大可选和 

int main(){
    //加快读写 
    ios::sync_with_stdio(false);
    cin.tie(0);
    cout.tie(0);
    cin >> n;
    for(int i = 1;i <= n;++i)
        cin >> nums[i];

    f[1] = nums[1];
    f[2] = max(nums[1],nums[2]);
    for(int i = 2;i <= n;i++)
        f[i] = max(nums[i]+f[i-2],f[i-1]);
    cout << f[n] << endl;

    return 0;
}